9 RRLL: Functional Grids
Racket Rogue-Like Library: Functional Grids
These modules provide the purely functional immutable grid implementations. The main differences are memory consumption and the time and memory complexity of referencing or setting a tile to a new value.
9.1 Generics
| (require rrll/grid/generics) | package: rrll-grid |
The generic interface deals only with accessing and modifying the grid. On top of this interface more common functionality is added.
(rlgrid-ref grid x y) - retrieves tile at given coordinates
(rlgrid-set grid x y value) - sets tile at given coordinates to a new value
(rlgrid-width grid) - returns the width of the grid
(rlgrid-height grid) - returns the height of the grid
The structs implementing this generic interface can - and probably will - implement other means of inspection. Construction of the underlying data structures is not covered by this generic interface.
procedure
rlg : rlgrid? x : nonnegative-integer? y : nonnegative-integer?
procedure
rlg : rlgrid? x : nonnegative-integer? y : nonnegative-integer? v : any/c
procedure
rlg : rlgrid? x : nonnegative-integer? y : nonnegative-integer? v : any/c
procedure
rlg : rlgrid? x : nonnegative-integer? y : nonnegative-integer?
If no #:default is provided, the are is clipped against the grid.
If the clipped or given rectangle has zero area, an empty stream is returned.
If #:default is provided, the sequence always iterates over the whole rectangle requested, but for tiles outside the grid it returns the default value provided.
When #:with-xy is given, the sequence will always return three values: x and y coordinates and value of the tile.
If #:only-xy is requested, only x and y coordinate values are provided by the sequence. This is mainly useful without #:default to iterate over a clipped rectangle.
If either xend or yend is #f, they are substituded for the width and height of given grid respectively.
To iterate over all tiles in given grid:
(for ((tile (in-rlgrid grid))) ...)
The same iteration with coordinates passed to the for loop body:
(for (((x y tile) (in-rlgrid #:with-xy grid))) ...)
Clipping the iteration rectangle to the grid (will iterate over 2x2 rectangle in the upper left corner of the grid):
(for (((x y tile) (in-rlgrid #:with-xy grid -10 -10 2 2))) ...)
With #:default specified, it is possible to substitute meaningful value for tiles outside the grid:
(for ((tile (in-rlgrid #:default #f -1 -1 2 2))) ...)
To only clip given rectangle to the grid and iterate over the coordinates:
(for (((x y) (in-rlgrid #:only-xy grid -1 -1 2 2))) ...)
9.2 dtgrid: Deduplicated Tree Based Grid
| (require rrll/grid/dtgrid) | package: rrll-grid |
This module implements gen:rlgrid that stores the grid in a binary tree where any node can be collapsed if its two child nodes contain values that are equal? to each other of if the child nodes are both collapsed and their collapsed value is the same.
procedure
(make-dtgrid width height default [ #:force force]) → dtgrid? width : positive-integer? height : positive-integer?
default :
(or/c (not/c procedure?) (procedure-arity-includes/c 0) (procedure-arity-includes/c 2)) force : boolean? = #f
If the default is a procedure, it is evaluated when given cell is accessed. If the procedure accepts two arguments, the coordinates of the tile being constructed are passed to it.
If the two tiles in the same cons cell are equal?, the cell is collapsed and separate cells are not allocated. If an internal tree node cons cell contains two collapsed values which are equal? it is collapsed recursively up to root if possible.
The construction takes constant time as only the collapsed root cell is allocated.
However, if force is #t and the default is a procedure?, all the tiles are created upon creation.
procedure
(dtgrid-stats dtg) →
nonnegative-integer? nonnegative-integer? nonnegative-integer? nonnegative-integer? dtg : dtgrid?
The values are:
Cons cells,
Collapsed subtrees,
Default value subtrees,
Value cells.
Because this procedure uses default value procedure which is evaluated lazily, it is actually a constant-time shallow copy of original rlg.
9.3 vgrid: Vector-Based Grid
| (require rrll/grid/vgrid) | package: rrll-grid |
n=w\cdot h
Method |
| Time |
| Memory |
Make |
| \Theta(n) |
| \Theta(n) |
Ref |
| \Theta(1) |
| \Theta(1) |
Set |
| \Theta(n) |
| \Theta(n) |
This module implements gen:rlgrid that stores the grid in a one-dimensional vector. The tiles in a row are stored from left to right and the rows are concatenated from top to bottom linearly in the vector.
procedure
width : positive-integer? height : positive-integer?
default :
(or/c (not/c procedure?) (procedure-arity-includes/c 0) (procedure-arity-includes/c 2))
9.4 Utilities
| (require rrll/grid/utils) | package: rrll-grid |
This module contains simple utilities commonly used by various algorithms in other modules.
procedure
(rlgrid-values rlg [ xstart ystart xend yend #:default default #:conv conv]) → any rlg : rlgrid? xstart : fixnum? = 0 ystart : fixnum? = 0 xend : (or/c fixnum? #f) = #f yend : (or/c fixnum? #f) = #f default : any/c = #f conv : (-> any/c any/c) = (λ (v) v)
(define-values (tl t tr l c r bl b cr) (rlgrid-values grid 0 0 3 3))
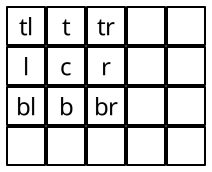
The conv routine is used to optionally convert the tiles as required.
(rlgrid-ref rlg (vec2-x v) (vec2-y v))
(rlgrid-set rlg (vec2-x p) (vec2-y p) v)
procedure
(rlgrid-component rlg x y [ #:directions dirs #:passable? passable?]) → (set/c vec2?) rlg : rlgrid? x : fixnum? y : fixnum? dirs : (listof vec2?) = vec2s:grid passable? : (-> any/c boolean) = (λ (v) v)
procedure
→
fixnum? fixnum? fixnum? fixnum? rlg : rlgrid? x0 : fixnum? y0 : fixnum? x1 : (or/c #f fixnum?) = #f y1 : (or/c #f fixnum?) = #f
procedure
(rlgrid-set-border rlg component [ #:directions dirs]) → (set/c vec2?) rlg : rlgrid? component : (set/c vec2?) dirs : (listof vec2?) = vec2s:grid
procedure
rlg : rlgrid? component : (set/c vec2?) pred? : (-> any/c boolean?)
procedure
(rlgrid-pass-neighbors rlg pos [ #:directions dirs #:passable? passable?]) → (listof vec2?) rlg : rlgrid? pos : vec2? dirs : (listof vec2?) = vec2s:grid passable? : (-> any/c boolean?) = (λ (v) v)
9.5 Discrete Differential Analysis
| (require rrll/grid/dda) | package: rrll-grid |
procedure
(dda rlg start-x start-y ray-dx ray-dy [ limit-t wall? skip-start-tile]) →
(or/c #f flonum?) any/c (or/c #f vec2?) rlg : rlgrid?
start-x :
(and/c (or/c fixnum? flonum?) (not/c negative?))
start-y :
(and/c (or/c fixnum? flonum?) (not/c negative?)) ray-dx : (or/c fixnum? flonum?) ray-dy : (or/c fixnum? flonum?) limit-t : (or/c fixnum? flonum?) = +inf.0 wall? : (-> any/c boolean?) = (λ (v) (not v)) skip-start-tile : boolean? = #t
![]()
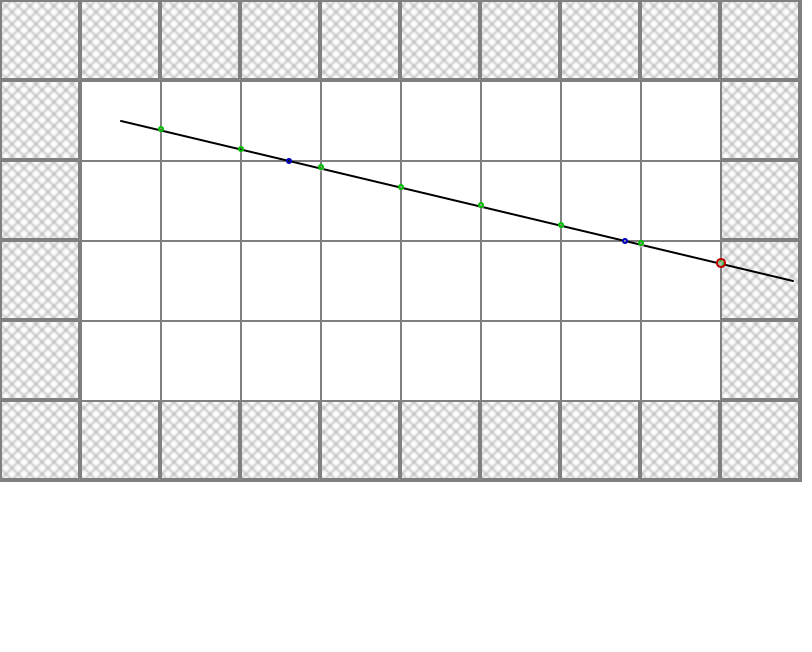
If any of the coordinates start-x, start-y, ray-dx, or ray-dy are integer?, they are adjusted to point to the center of given tile by adding 0.5 to their value.
The limit-t argument specifies maximum distance before giving up finding a collision and returning #f for all return values.
As the implementation expects a grid of boolean? values where #f means wall (impassable, opaque tile) and #t means free space (passable, transparent tile), the default predicate for wall? reflects that. This makes the algorithm easy to adapt to different representations.
If skip-start-tile is true, a hit within the starting tile is ignored.
The values returned are:
distance from the beginning of the ray to the hit
value of the tile that caused the ray hit
coordinates of this tile as vec2?
9.6 Visibility Arcs
| (require rrll/grid/varc) | package: rrll-grid |
This module implements visibility arcs, simple operations with them and method for determining tile arc from given center point.
It allows computing possibly visible tiles in a rlgrid?.
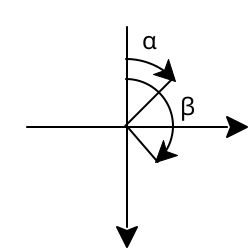
struct
(struct varc (start end))
start : flonum? end : flonum?
The starting angle \alpha and ending angle \beta are shown in the figure.
9.7 Computing Visibility Fans in Grids
| (require rrll/grid/vfan) | package: rrll-grid |
procedure
(vfan-iter rlg start-x start-y proc [ #:wall? wall? #:init-varc init-varc #:with-tile with-tile #:process? process?]) → void? rlg : rlgrid? start-x : real? start-y : real? proc : (-> fixnum? fixnum? void?) wall? : (-> any/c boolean?) = (λ (v) (not v)) init-varc : varc? = full-varc with-tile : boolean? = #f process? : (-> any/c boolean?) = (λ (v) #f)
For each tile covered by the visibility fan centered upon the starting point it evaluates given proc with the X and Y coordinate of such tile being the only arguments provided (for now).
The #:wall? keyword argument can be used to specify how the algorithm recognizes which walls are opaque for the purpose of visibility computation.
The init-varc argument can be used to limit the initial search arc to particular direction and field-of-view.
If with-tile is #t, the proc gets always evaluated with a third argument - the tile in question - as well.
When process? returns non-#f for any tile that is considered wall, it is processed with proc although it does not add any tiles to further iteration.
syntax
option = #:with-tile | #:wall? wall? = (λ (v) (not v)) | #:process? process? = (λ (v) #f) | #:dir dir = #f | #:fov/2 fov/2 = #f | #:init-varc init-varc = full-varc
rlg : rlgrid?
start-x : flonum?
start-y : flonum?
wall? : (-> any/c boolean?)
dir : (or/c #f flonum?)
fov/2 : (or/c #f flonum?)
init-varc : varc?
The dir and fov/2 arguments have precedence over init-varc if they are both specified.